
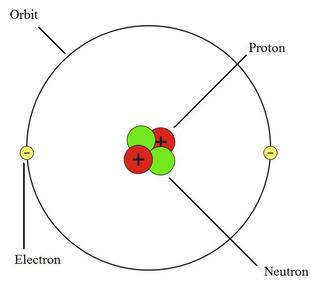
The presence of only one electron made it quite difficult to choose a correct solution for a single dipole moment. In the previous part, we indicated that for a Hydrogen atom the differential approach can produce several types of solutions. In Project 2, we shall address these problems and discuss other questions. The nature of that difference is not discussed. It is different atomic orbit configurations with different sets of energy levels. That is why besides the circular shape of the electron orbit there is no calculation of the actual shape of the electrons orbit in a Helium atom.Įxperiments prove that in the case of a Helium atom the difference between ortho-Helium and para-Helium is not restricted to having opposite spin. Electron orbit is calculated as the convolution of the shape of the orbital and the experimentally suggested shape of spherical shells.įor a Helium atom, that approach does not work. Quantum Mechanical orbitals indicate that the maximum probability density to find an electron in an atom is located inside the proton in a Hydrogen atom. Introduction & the Current state of the problem. In the same approach as we used for the Hydrogen atom orbit we do not need to use the Quantum Mechanical Orbital Postulate, Pauli Postulate or any other postulates. Bohr used for his model of the Hydrogen atom, but we do not use operators, so we are not bound by the statistical characteristics of the Uncertainty Principle. We use Quantum Mechanics the same way as N. Electron spins behave similar to a compass, which aligns along the stronger magnetic field.Ĭomplicated energy spectra of a Helium atom gets a simple explanation in the terms of two types of orbits and two sets of energy levels for the ortho- and para- Helium.
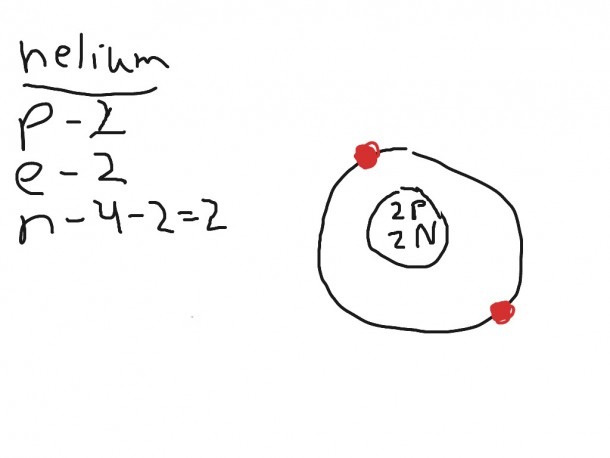
In our model, electron spins are aligned along the magnetic fields created by the orbital movement of electrons. They can have directions toward and away from the center of the nucleus. Orbital moments of electrons in our model align along the radii of the electrons orbits. Our model explains Pauli Principle, but does not need a postulate. We demonstrate that actual directions of spins are radial directions toward the center of the nucleus and away from the center of the nucleus. This Principle needs to be postulated in Quantum Mechanics, because it contradicts both the Law of Energy Conservation and also Electrostatics. The Pauli Principle postulates electrons spin directions as up and down. We combine Electrodynamics and Quantum Mechanics in order to calculate the exact parameters of orbits. Magnetic fields induced by rotating electrons are simply ignored. Quantum Mechanical expressions for Hamiltonians for both Helium and Hydrogen do not include the term for Maxwell Electrodynamics. We explain why the ground state of a Helium atom is not the lowest energy state. Both para- and ortho- configurations of electron orbits are analyzed. We present here a simple solution as well as a detailed image of an electrons orbits in Helium atoms. Additional restrictions can be used for model control, because ortho- and para- configuration of electron orbits have their specific sets of energy levels. In the case of the Helium atom, there is only one solution for two electrons, which create both dipole and quadrupole moments. Taking into account that the Hydrogen atom has only one electron, our solution was not strictly the only possible solution for the electron orbit. Our analysis of the electron orbit for a Helium atom repeats several aspects of our analysis of the electron orbit of a Hydrogen atom, because these are the same types of orbits. The straight lines originated from the nucleus show the directions of orbital moments and the directions of induced magnetic fields for each electron.
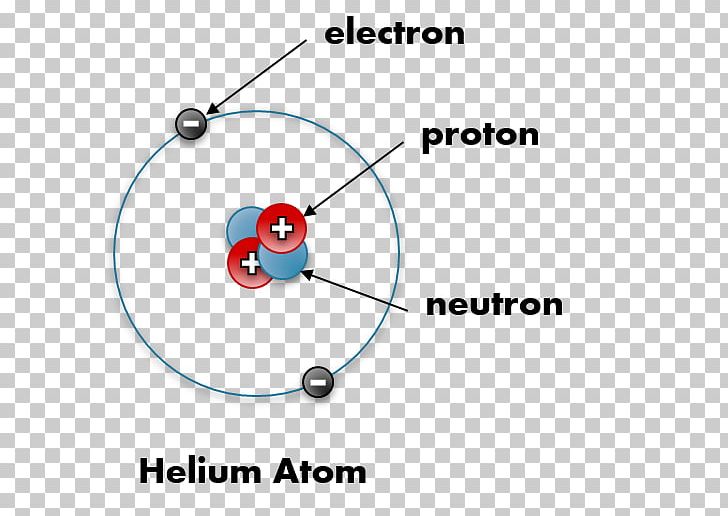
The orbits of two electrons are shown with different colors (first electron – blue, second electron – green). The shape of electrons orbits of a Helium atom in the para- configuration, which corresponds to the ground state of an atom.


 0 kommentar(er)
0 kommentar(er)
